Lecture: 25 - 26

[ Home ][ PDF ]

Topics: Basics of coding theory

• Introduction
• Definitions:
  • Codewords
  • coding and decodings schemes
  • message symbols
  • control symbols
• Definitions of Linear Code
  • Linear code, its length and dimention
  • Parity Check matrix and parity check equations
  • Binary and systematic codes
  • Example 9.1, 9.3 (parity-check code) and 9.4 (repitition code)
• Definition of error words
  • (error vector)
  • Hamming distatnce and Hamming weight
  • Lemma 9.9 on Properties of Hamming distatnce
• Definition of t-error-correcting
  • Minimum distance of linear code
  • Theorem 9.12 on connection between error correcting and minimum distance
• Special type of codes:
  • Binary Hamming code (def 9.22)
  • Cyclic code (def 9.35)

Introduction

One of the major application of finite files is coding theory. This theory has its origin in a famous therorem of Shannon that guarantees the existence of code that can transmit information at rates close to capacity with an arbirariuly small probability of error. On purpose of algebraic coding theory, the theory of error-correcting and error-detecting codes, is to devie methonds for the contruction of such codes.

During the last two decades more and more abstract algebraic tools such as the theory of finite fields and polynomials over finite fileds have indluenced coding.

In particular the description on redundant codes by polynomials over $\mathbb{F_q}$ is a milestone in this development. Thefact tath one can use shift registers for coding and decoding establishes a connection with linear recurring sequences.

Linear Codes

The problem of the communication of information , in particular the coding and decoding of information for the reliable transmission over a “noisy” channel, is of great importance today.

Typically, one has to transmit a message which consists of a finite sequence of symbols that are elements of some finite alphabet. For instance, if this alphabet consists simply of $0$ and $1$, the message can be described as a binary number.

Generally the alphabeth is assumned to be a finite field.

Now the transmission of finite sequences of elements of the alphabeth over a communication channel need not be perfect in the sense that each bit of information is transmitted unaltered over this channel.

As there is no ideal channel without “noise” the receiver of the transmitted may obtain distorted information and may make errors in interpreting the transmitted signal.

One of the main problems of coding theory is to make the errors, which occur for instance because of noisy channels, extremly imrobable. The methods to improve the reliability of transmission depend on properties of finite fields.

A basic idea in algebraic coding throry is to transmit redundant information together with the message one wants to communicate; that is one extends the sequence of message symbols to a longer sequence in a systematic maner.

A simple model of communication system is shown in figure.

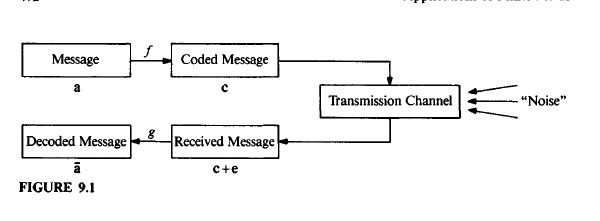
We assume that the symbols of the message and of the coded message are elemens of the same finite field $\mathbb{F_q}$.

Coding means to encode a block of $k$ message symbols $a_1a_2 \dots a_k, a_i \in \mathbb{F_q}$ into a code word $c_1c_2 \dots c_n$ of $n$ symbols $c_j \in \mathbb{F_q}$ where $n > k$.

We regard the code word as an $n$-dimentional row vector $\vec{c} \in \mathbb{F_q}^n$.

Thus $f$ in the figure is a function from $\mathbb{F_q}^k$ into $\mathbb{F_q}^n$ called a coding scheme, and $g: \mathbb{F_q}^n \rightarrow \mathbb{F_q}^k$ is a decoding scheme.

A simple type of coding scheme arises when each block $a_1a_2 \dots a_k$ of message symbols is encoded infto a code word of the form:

$$a_1a_2 \dots a_kc_{k+1} \dots c_k$$

where the first $k$ symbols are the original message symbols and the additional $n -k$ symbols in $\mathbb{F_q}$ are control symbols. Such coding schemes are often presented in the following way.

Let $H$ be a given $(n-k)\times n$ matrix with entries in $\mathbb{F_q}$ that is of the special form:

$$H = (A, I_{n-k})$$

where $A$ is an $(n-k)\times k$ matric and $I_{n-k}$ the identity matric of order $n-k$. The control symbols $c_{k+1}, \dots, c_k$ can be calculated from the system of equations:

$$H\vec{c}^T = \vec{0}$$

for code words $\vec{c}$. The equations of this system are called parity-check-equations.

Example

Let $H$ be the following $3\times7$ matrix over $\mathbb{F_2}$:

$$H = \begin{bmatrix} 1 & 0 &1 &1 &1 &0 &0 \\ 1 & 1 &0 &1 &0 &1 &0 \\ 1 & 1 &1 &0 &0 &0 &1 \\ \end{bmatrix}$$

Then the control symbols can be calculated by solving:

$$H\vec{c}^T = \vec{0}$$

given $c_1,c_2,c_3,c_4$:

$$\begin{bmatrix} c_1 & & + c_3 &+ c_4 & +c_5 & & & = 0 \\ c_1 & + c_2 & & +c_4 & & +c_6 & & =0 \\ c_1 & + c_2 & +c_3 & & & & +c_7 &= 0 \end{bmatrix}$$

The control symbols $c_5, c_6,c_7$ can be expressed as:

$$\begin{bmatrix} c_5 =& c_1 & & + c_3 &+ c_4 & \\ c_6 =& c_1 & + c_2 & & +c_4 \\ c_7 =& c_1 & + c_2 & +c_3 & \\ \end{bmatrix}$$

Thus the coding scheme in this case is a linear map from $\mathbb{F_2^4}$ into $\mathbb{F_2^7}$ given by:

$$(a_1,a_2,a_3,a_4) \rightarrow (a_1,a_2,a_3,a_4, a_1+a_3+a_4, a_1+a_2+a_4, a_1+a_2+_a3)$$

In general, we use the following terminology in connections with coding schemes that are given by linear maps.

Definition 9.2

Let $H$ be an $(n-k) \times n$ matrix of rank $n-k$ with entries in $\mathbb{F_q}$.

The set $C$ of all $n$-dimentional vectors $\vec{c} \in \mathbb{F_q}^n$ such that $H\vec{c}^T = \vec{0}$ is called a linear $(n,k)$ code over $\mathbb{F_q}$. $n$ is called the length $k$ is called the dimention of the code.

The elements of $C$ are called code words (or code vectors), the matrix $H$ is a parity-check matric of $C$.

If $q = 2$,$C$ is called a binary code. If $H$ is of the form $(A, I_{n-k})$ , then $C$ is called a systematic code.

Systematic code (from wiki): “In coding theory, a systematic code is any error-correcting code in which the input data is embedded in the encoded output. Conversely, in a non-systematic code the output does not contain the input symbols.”

We note that the set $C$ of solutions of the system $H\vec{c}^T=\vec{0}$ of linear equactions is a subspace of dimension $k$ of the vector space $\mathbb{F_q}^n$.

Since the code words form an additive group, $C$ is also called a group code. Moveover $C$ can be regarded as the null space of the matrix $H$.

Example 9.3 (Parity-check Code)

Let $q=2$ and let the given message be $a_1,a_2,\dots,a_k$ then the coding scheme $f$ is defined by:

$$f : a_1 \dots a_k \rightarrow b_1 \dots b_{k+1}$$

where $b_i = a_i$ for $i = 1, \dots, k$ and:

$$b_{k+1} = \begin{cases} 0 , \text{ if } \sum_{i=1}^{k} a_i = 0,\\ 1, \text{ if } \sum_{i=1}^k a_i = 1 \end{cases}$$

Hence it follows that the sum og digits of any code word $b_1 \dots b_{k+1}$ is $0$. If the sum of digits of the received word is $1$. then the receiver knows that a transmission error must have occurred.

Let $n = k +1$, then this code is a binary linear $(n, n-1)$ code with parity-check matrix $H = (1 1 \dots 1)$.

Example 9.4 (Repetition code)

In a repetition code each code word consists of any one message symbol $a_1$ and $n-1$ control symbols $c_2 = \dots = c_n$ all equal to $a_1$. That is $a_1$ is repeated $n-1$ times.

This is a linear $(n,1)$ code with parity-check matrix $H=(-1, I_{n-1})$

The parity-check equations $H\vec{e}^T = \vec{0}$ with $H = (A, I_{n-k})$ imply:

$$\vec{c}^T = \begin{bmatrix} I_{k} \\ -A\end{bmatrix} \vec{a}^T$$ $$= \begin{bmatrix} \vec{a}(I_k, -A^T) \end{bmatrix}^T$$

where $\vec{a} = a_1, \dots , a_k$ is the message and $\vec{c} = c_1, \dots , c_n$ is the codeword. The leads to the following definition:

Definition

The $k\times n$ matrix $G = (I_k, -A^T)$ is called canonical generator matrix of a linear $(n,k)$ code with parity-check matrix $H=(A,I_{n-k})$.

From $H\vec{e}^T = \vec{0}$ and $\vec{c} = \vec{a}G$ it follows that $H$ and $G$ are related by:

$$GH^T = \vec{0}$$

The code $C$ is equal to the row space of the canonical generator matrix $G$. More genreally, any $k\times n$ matrix $G$ whose row space is equal to $C$ is called a generator matrix of $C$.

Example Generator Matrix

Let $H$ be the following $3\times7$ matrix over $\mathbb{F_2}$:

$$H = \begin{bmatrix} 1 & 0 &1 &1 &1 &0 &0 \\ 1 & 1 &0 &1 &0 &1 &0 \\ 1 & 1 &1 &0 &0 &0 &1 \\ \end{bmatrix}$$

The canonical generator matrix for the code defined by $H$ is given by:

$$G = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 \end{bmatrix}$$

Definition (error word/vector)

If $\vec{c}$ is a code word and $\vec{y}$ is the received word after communication through a “noisy” channel, then $\vec{e} = \vec{y} - \vec{c} = e_1 \dots e_n$ is called the error word or the error vector

Definition

Let $\vec{x},\vec{y}$ be two vectors in $\mathbb{F_q}^n$. Then:

• The Hamming distatnce $d(\vec{x},\vec{y})$ between $\vec{x}$ and $\vec{y}$ is the number of coordinates in which $\vec{x}$ and $\vec{y}$ differ:
• The Hamming weight $w(\vec{x})$ of $\vec{x}$ is the number of nonzero coordinates of $\vec{x}$.

Thus $d(\vec{x}, \vec{y})$ gives the number of errors if $\vec{x}$ is the transmitted code word and $\vec{y}$ is the received word. If follows immediataly that $w(\vec{x}) = d(\vec{x}, \vec{0})$ and $d(\vec{x},\vec{y}) = w(\vec{x} - \vec{y})$.

Lemma Hamming distance

The Hamming distance is a metric on $\mathbb{F_q}^n$. That is for all $\vec{x},\vec{y},\vec{z} \in \mathbb{F_q}^n$ we have:

• $d(\vec{x},\vec{y}) = 0 $ if and only if $\vec{x} = \vec{y}$
• $d(\vec{x}, \vec{y}) = d(\vec{y}, \vec{x})$
• $d(\vec{x},\vec{z}) = d(\vec{x},\vec{y}) + d(\vec{y}, \vec{z})$

In decoding received words $\vec{y}$, one usually tries to find the code word $\vec{c}$ such taht $w(\vec{y}-\vec{c})$ is as small as possible, that is, one assumes that it is more likely that few errors have occurred rather than many. Thus in the decoding we are looking for a code word $\vec{c}$ that is closets to $\vec{y}$ according to the Hamming distance.

This rule is called nearest neighbor decoding.

Definition (t-error-correction)

For $t \in \mathbb{N}$ a code $C \subseteq \mathbb{F_q}^n$ is called a t-error_correcting if for any $\vec{y} \in \mathbb{F_q}^n$ there is at most one $\vec{c} \in C$ such that $d(\vec{y}, \vec{c}) \leq t$

If $\vec{c} \in C$ is transmitted and at most $t$ errors occur, then we have $d(\vec{y}, \vec{c}) \leq t$ for the recived word $\vec{y}$. If $C$ is t-error-correcting then for all other code words $\vec{z} \neq \vec{c}$ we have $d(\vec{y}, \vec{z}) > t$ which means taht $\vec{c}$ is closest to $\vec{y}$ and nearest neighbor decoding gives the correct result. Therefor, one aim in coding throry is to construct codes with code words “far apart”. On the other hand, one tries to transmit as much information as possible. To reconcile these two aims is one of the problems of coding.

Def: Minimum distatnce of the linear code.

The number:

$$d_C = \min\limits_{\vec{u},\vec{v} \in C, \vec{u} \neq \vec{v}} d(\vec{u},\vec{v}) = \min \limits_{\vec{0} \neq \vec{c} \in C} w(\vec{c})$$

is called the minimum distatnce of the linear code $C$.

Theorem

A code $C$ with minimum distance $d_C$ can correct up to $t$ errors if $d_C \geq 2t + 1$

Proof:

A ball $B_t(x)$ of radius $t$ and center $x \in \mathbb{F_q}^n$ consists of all vectors $\vec{y} \in \mathbb{F_q^n}$ such that $d(\vec{x}, \vec{y}) \leq t$. The nearest neighbor decoding rule ensures that each received word with $t$ or fewer errors must be in a ball of radius $t$ and center the transmitted code word. To correct $t$ errors, the balls with code words $\vec{x}$ as centers must not overlap. If $\vec{u} \in B_t(\vec{x})$ and $\vec{u} \in B_t(\vec{y})$, $\vec{x},\vec{y} \in C, \vec{x} \neq \vec{y}$ then:

$$d(\vec{x},\vec{y}) \leq d(\vec{x}, \vec{u}) + d(\vec{u}, \vec{y}) \leq 2t$$

a contradiction to $d_C \geq 2t+1 $

Example

Let $H$ be the following $3\times7$ matrix over $\mathbb{F_2}$:

$$H = \begin{bmatrix} 1 & 0 &1 &1 &1 &0 &0 \\ 1 & 1 &0 &1 &0 &1 &0 \\ 1 & 1 &1 &0 &0 &0 &1 \\ \end{bmatrix}$$

The code has minimum distatnce $d_C = 3$ and therefore can correct one error.

Lemma

This lemma is useful in determining the minimum distance of a code.

A linear code $C$ with parity-check matrix $H$ has minimum distatnce $d_C \leq s + 1$ if and only if any $s$ columns of $H$ are linearly independent.

Proof:

Assume there are $s$ linearly dependent columns of $H$, then $H\vec{c}^T = \vec{0}$ and $w(\vec{c}) \leq s$ for suitable $\vec{c} \in C, \vec{c} \neq \vec{0}$, hence $d_C \leq s$. Similarly, if any $s$ columns of $H$ are linearly independent, then there is no $\vec{c} \in C , \vec{c} \neq \vec{0}$ of weight $leq s$ hence $d_C \geq s + 1$.

Next we describe a simple decoding algorithm for linear codes. Let $C$ be a linear $(n,k)$ code over $\mathbb{F_q}$. The vector space $\mathbb{F_q}^n/C$ consists of all cosets $\vec{a} + C = {\vec{a} + \vec{c}: \vec{c} \in C }$ with $\vec{a} \in \mathbb{F_q}^n$

Each coset contains $q^k$ vectors and $\mathbb{F_q}^n$ can be regarded as being partitioned into cosets of $C$:

$$\mathbb{F_q}^n = (a^{(0)}+C) \cup (a^{(1)}+C) \cup \dots \cup (a^{(s)}+C)$$

where $\vec{a}^{(0)} = \vec{0}$ and $s = q^{n-k}-1$. A received vector $\vec{y}$ must be in one of the cosets, say in $\vec{a}^{(i)} + C$.

If the code word $\vec{c}$ was transmitted, then the error is given by $\vec{e} = \vec{y} - \vec{c} = \vec{a}^{(i)} + \vec{z} \in \vec{a}^{(i)} + C$ for a suitable $\vec{z} \in C$. This leads to the following decoding scheme.

Decoding of Linear Codes.

All possible errors vectors $\vec{e}$ of a received vector $\vec{y}$ are the vectors in the coset of $\vec{y}$. The most likey error vector is the vector $\vec{e}$ with minimum weight in the coset of $\vec{y}$. Thus we decode $\vec{y}$ as $\vec{x} = \vec{y} - \vec{e}$. The implementation of this procedure can be facilitated by the coset-leader algorithm for error correction of linear codes.

Binary Hamming Code

Definition: A binary $C_m$ of length $n = 2^m-1, m \geq 2$ with and $m \times (2^m-1)$ parity-check matrix $H$ is called a binary Hamming Code if the columns of $H$ are binary representations of the integers $1,2,\dots, 2^m-1$.

Lemma

$C_m$ is a 1-error-correcting code of deimention $2^m-m-1$

Proof

By definition of the parity check matrix $H$ of $C_m$, the rank of $H$ is $m$. Also any two columns of $H$ are linearly independent. Since $H$ contains with any two of its columns also their sum, the minimum distaticen of $C_m$ equals $3$. Thus $C_m$ is 1-error-correcting.

Example:

Let $C_3$ be the $(7,4)$ Hamming Code with parity-check matrix:

$$H = \begin{bmatrix} 0 & 0 & 0 &1 &1 &1 &1 \\ 0 & 1 & 1 &0 &0 &1 &1 \\ 1 & 0 &1 &0 &1 &0 &1 \\ \end{bmatrix}$$

If the syndrome of a received word $\vec{y}$ is $S(\vec{y}) = (1 0 1 )^T$, then we know that the an error must have occurred in the fift position, since $101$ is the binary representation of $5$.

Cyclic codes

Cyclic vodes are special class of linear codes that can be implemented fairly simply and whose mathematical structure is reasonably well known.

Definition

A linear $(n,k)$ code $C$ over $\mathbb{F_q}$ is called cyclic if $(a_0,a_1, \dots ,a_{n-1}) \in C $ implies $(a_{n-1}, a_0, \dots , a_{n-2}) \in C$

From now on we impose the restriction $\gcd(n,q) =1$ and let $(x^n-1)$ be the ideal generated by $x^n-1 \in \mathbb{F_q}[x]$. Then all elements of $\mathbb{F_q}[x]/(x^n-1)$ can be represented by polynomials of defree less than $n$ and clearly this residue class ring is isomorphic to $\mathbb{F_q}^n$ as a vector space over $\mathbb{F_q}$. An isomophism is given by:

$$(a_0, a_1, \dots , a_{n-1}) \iff a_0 + a_1x+ \dots +a_{n-1}x^{n-1}$$

Because of this isomoerphism, we denote the elements of $\mathbb{F_q}[x]/(x^n-1)$ either as polynomials of defree $< n \mod x^n -1$ or as vectors or words over $\mathbb{F_q}$.

We introduce multiplication of polynomials modulo $x^n-1$ in the usual way; that is, if $f \in \mathbb{F_q}[x]/(x^n-1), g_1, g_2 \in \mathbb{F_q}[x]$, then $g_1g_2 = f$ means that $g_1g_2 \equiv f \mod (x^n-1)$.

A cyclic $(n,k)$ code $C$ can be obtained by multiplying each message of $k$ coordinates (identified with a polynomial degree $< k $) by a fixed polynomial $g(x)$ of degree $n-k$ with $g(x)$ a diviso og $x^n-1$. The polynomial $g(x), xg(x), \dots, x^{k-1}g(x)$ corresponds to code words of $C$.

A generator matrix of $C$ is given by:

$$G = \begin{bmatrix} g_0 & g_1 & \dots & g_{n-kl} & \dots & 0 & 0 & \dots & 0 \\ 0 & g_0 & g_1 & \dots & \dots & g_{n-k} & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & & \vdots & & & &\vdots\\ 0 & 0 & 0 & \dots & 0 & g_0 & g_1 & \dots & g_{n-k}\\ \end{bmatrix}$$

Where $g(x) = g_0 + g_1x + \dots + g_{n-k}x^{n-k}$.

The rows of $G$ are obviously linear independent and rank$(G) = k$, the dimention of $C$.

If $h(x) = (x^n-1)/g(x) = h_0 + h_1x + \dots + h_kx^k$ then we see that the matrix:

$$H = \begin{bmatrix} 0 & 0 & \dots & \dots & 0 & h_k & h_{k-1} & \dots & \dots & h_0 \\ 0 & 0 & \dots & 0 & h_k & h_{k-1} & & \dots & h_0 & 0 \\ \vdots & \vdots & & & & & & & & \vdots \\ h_k & h_{k-1} \cdots & \cdots & h_0 & 0 & \cdots & \cdots & \cdots & \cdots & 0 \end{bmatrix}$$

is a parity-check matrix for $C$.

The code with generator matrix $H$ is the dual code of $C$ whick is again cyclic.