Lecture: 23 -24

[ Home ][ PDF ]

Topics: Boolean functions pt 2

These lectures are dedicated to vectorial Boolean functions used in cruptography in block ciphers. Two most powerful attacks on block ciphers are differential and linear attacks and functions optimal agains both of them are bent and almost bent (AB) functions, and functions optimal agianst differential attakc are almost perfect nonlinear (APN) functions.

Every AB function is APN, the converse it not true in general: there are examples of APN functions which are not AB, but all quadratic APN functinos are necessarily AB.

Checking APN and AB properties of functions is difficult in general but it is simpler for the cases of quadratic and power functions.

There are severeal characterisations of APN and AB functions (necessary and sufficient conditions), in particular, via Walsh transform.

There are different equivalence relations which have APN and AB properties as invariants. That is, if a function $F$ is APN (or AB) and $F’$ is equivalent to it, then $F’$ is APN (respectivly AB) too. Linear, affine, cyclotomic, EA, EAI and CCX equivalences are among them.

These equivalences relations relate to each other in some ways, for example, all these equivalences are particular cases of CCZ-equivalence.

Differantial Uniformity and APN Functions

Differential Uniformity and Derivatives of Functions

Differential cryptoanalysis of block ciphers was introduced by Biham and Shamir in 1991.

$F: \mathbb{F_2^n} \rightarrow \mathbb{F_2^n}$ is a differential $\delta$-uniform if:

$$F(x + a) + F(x) = b, \forall a \in \mathbb{F_{2^{n}}^*}m, \forall b \in \mathbb{F_{2^{n}}^*}m$$

and it has at most $\delta$ solutions.

Differential uniformity measures the resistance the resistatnace to differential attack. The smaller $\delta$ the better the resistance.

The derivative of $F$ in direction $a\in \mathbb{F_{2^n}^*}$ is

$$D_aF(x) = F(x + a) + F(X)$$

$\delta_F(a,b)$ denotes the number of solutions of $F(x+a) + F(x) = b$

Almost Perfect Nonlinear Functions

F is almost perfect nonlinear (APN) if $\delta = 2$.

APN functions are optimal for differential cryptoanalysis

First example of APN functions [Nyberg 1993]:

• Gold function $x^{2^i+1}$ on $\mathbb{F_{2^n}}$ with $\gcd(i,n) = 1$
• Inverse function $x^{2^n-2}$ on $\mathbb{F_{2^n}}$ with $n$ odd.

Necessary and Sufficient Conditions for APN

$$|\{ F(x+a) + F(x) : x \in \mathbb{F_{2^n}}\} | = 2^{n-1}$$

for any $a \in \mathbb{F_{2^n}^*}$

$D_aF$ is a two-to-one mapping for any $a \neq 0$

For every $(a,b) \neq 0$ the system: $\begin{cases} x + y = a\\ F(x) + F(y) = b, \end{cases}$

admints $0$ or $2$ solutions.

The funtion $\gamma_F: \mathbb{F_{2^n}^2} \rightarrow \mathbb{F_2}$ defined by:

$$\gamma_F(a,b) = \begin{cases} 1, \text{if } a\neq 0 \text{ and } \delta_F(a,b) \neq 0 \\ 0 \text{ otherwise} \end{cases}$$

has weight $2^{2n-1} -2^{n-1}$

Quadratic and Power APN Functions

$ F(x) = x^d$ on $\mathbb{F_{2^n}}$ then $F$ is APN iff $D_1F$ is a two-to-one mapping. Indeed, for any $a \neq 0$

$$DaF(x) = (x+a)^d + x^d$$ $$= a^d((\frac{x}{a} + 1)^d + (\frac{x}{a})^d)$$ $$= a^d D_1F(\frac{x}{a})$$

If $F$ is quadratic then $F$ is APN if and only if:

$F(x + a) + F(x) = F(a)$has 2 solutions for any $a \neq 0$

Example:

$F(x) = x^9$ is APN over $\mathbb{F_{2^n}}$ then $\gcd(3,n) = 1$ since $F$ is quadratic power function and thus it is enough to consider:

$F(x +1) + F(x) = F(1)$, that is $(x +1)^9 +x^9 = 1$

Which gives $x^8 = x$ or, equivalently $x^7 = 1$ when $x \neq 0$.

Hence $\gcd(7,2^n-1) =1$ then $F(x+1) + F(x) = F(1)$ has only two colutions $0$ and $1$.

Nonlinearity and AB Functions

Nonlinearity of Functions

Linear cryptoanalysis was discovered by Matsui in 1993. Distatnce between two boolean functions:

$$d(f,g) = |\{ x \in \mathbb{F_{2^n}} : f(x) \neq g(x)\} |$$

Nonlinearity of $F: \mathbb{F_{2^n}} \rightarrow \mathbb{F_{2^m}}$:

$$N_F = \min\limits_{a\in\mathbb{F_{2^n}}, b\in\mathbb{F_2}, v\in\mathbb{F_{2^m}^*}} D(tr_m(v F(x), tr_n(ax) + b)$$

Nonlinearity measures the resistance to linear attack [Chabaud and Vaudenay 1994].

Walsh Transform of an $(n,m)$-function $F$

$$\lambda_F(u,v) = \sum_{x\in \mathbb{F_{2^n}}} (-1)^{tr_m(v F(x)) + tr_n(ux)}, u \in \mathbb{F_{2^n}}, v \in \mathbb{F_{2^m}^*}$$

Walsh coefficients of $F$ are the values of its Walsh Transform Walsh spectrum of $F$ is the multi-set of all Walsh coefficients of $F$

The extended Walsh spectrum of $F$ is the multi-set of absolute values of all Walsh coefficients of $F$

Walsh Tansform and APN Functions

For any $(n,n)$-function $F$:

$$\sum_{a,b\in\mathbb{F_{2^n}}} \delta_F(a,b)^2 = \frac{1}{2^{2n}}\sum_{a,b\in\mathbb{F_{2^n}}} \lambda_F(a,b)^4$$

$F$ is APN if and only if:

$$\sum_{u,v\in\mathbb{F_{2^n}}, v\neq 0} \lambda_F^4(u,v) = 2^{3n+1}(2^n-1)$$

The nonlinearity of $F$ via Walsh Transform

$$N_F = 2^{n-1} - \frac{1}{2} \max\limits{u\in\mathbb{F_2^n},v\in\mathbb{F_{2^m}^*}} | \lambda_F(u,v) |$$

Covering radius bounds for an $(n,m)$-function $F$:

$$N_F \leq 2^{n-1} - 2^{n/2-1}$$

$N_F \leq 2^{n-1} - 2^{n/2-1}$ if and only if $\lambda_F(u,v) = \pm 2^{n/2}$ for any $u\in \mathbb{F_2^n}, v\in \mathbb{F_{2^m}^*}$

Then $F$ is called bent.

Bent $(n,m)$-functions exists if and only if $n$ is even and $m \leq n/2$

Almost Bent Functions

Sidelnikov-Chabaud-Vaudenay bound for $m \geq n-1$:

$$N_F \leq 2^{n-1} - \frac{1}{2} \sqrt{3 \cdot 2^n - 2 -2 \frac{(2^n-1)(2^{n-1}-1)}{2^m-1}}$$

It is tight only for $m = n$ and $(n,n)$-functions achive this bound have: $N_F = 2^{n-1} - 2^{\frac{n-1}{2}}$ and are called almost bent (AB).

AB functions are optimal for linear cryptanalysis $F$ is AB if and only if $\lambda_F(u,v) \in { 0, \pm 2^{\frac{n+1}{2}}}$

AB functions exists only for $n$ odd.

$F$ is maximally nonlinear if $n = m$ is even and $N_F = 2^{n-1} -2^{\frac{n}{2}}$ (conjectured optimal)

If $F$ is AB then it is APN . If $n$ is odd and $F$ is quadratic $APN$ then $F$ is $AB$. Algebraic degrees of AB functions are upper bounded by $\frac{n+1}{2}$

First example of AB functions:

• Golden ration $x^{2^i-1}$ on $\mathbb{F_{2^n}}$ with $\gcd(i,n) = 1,n$ is odd.
• Golden APN functoins with $n$ even are not AB
• Inverse fuciont are not AB.

Necessary and Sufficient Conditions for AB

For evyer $a,b \in \mathbb{F_{2^n}}$ the system of equations-:

$$\begin{cases} x + y + z = a \\ F(x) + F(y) + F(z) = b \end{cases}$$

Has $3 \cdot 2^2 -2$ solutions if $b = F(a)$ and $2^n -2$ otherwise.

The function $\gamma_F : \mathbb{F_{2^n}^2} \rightarrow \mathbb{F_2}$

$$\gamma_F(a,b) = \begin{cases} 1, \text{ if } a \neq \text{ and } \delta_F(a,b) \neq 0 \\ 0 \text{ otherwise } \end{cases}$$

is bent

$F$ is APN and all its Walsh coefficients are dicisible by $2^{\frac{n+1}{2}}$

Almost Bent Power Functions

In general, checking Walsh Spectrum for power functions is sufficient for $a\in \mathbb{F_2}$ and $b \in \mathbb{F_{2^n}^*}$

$F(x) = x^d$ is AB on $\mathbb{F_{2^n}}$ if and only if $\lambda_F(a,b) \in {0, \pm 2^{\frac{n+1}{2}}}$ for $a \in \mathbb{F_2}, b \in \mathbb{F_{2^n}^}$ since $\lambda_F(a,b) = \lambda_F(1, a^{-d}b)$ for $a\in \mathbb{F_{2^n}^}$

In the case of a power permutation it, it suffices to check (the Walsh spectrum) for $b = 1$ and all $a$.

If $F = x^d$ is a permutation, $F$ is AB if and only if:

$\lambda_F(a,1) \in { 0, \pm 2^{\frac{n+1}{2}} }$ for $a \in \mathbb{F_{2^n}}$, since $\lambda_F(a,b) = \lambda_F(ab^{-\frac{1}{d}},1)$

Equivalence Relations of Functions

Important of Equivalence Relations for Functions

Equivalence relations preserving main cryptographic properties (APN and AB) divide the set of all functions into classes.

They can be powerful construction methods providing for each function a huge class of functionss with the same properties.

Instead of checking invariant properties for all functions, it is enough to check only one in each class.

Cyclotomic, Linear, Affine, EA- and EAI- Equivalences

$F$ and $F’$ are affine (resp. linear) equivalent if

$$F' = A_1 \circ F \circ A_2$$

for some affine (resp. linear) permutation $A_1$ and $A_2$.

$F$ and $F’$ are extended affine equivalent (EA-Equivalent):

$$F' = A_1 \circ F \circ A_2 + A$$

for some affine permutations $A_1$ and $A_2$ and some affine $A$

$F$ and $F’$ are EAI-equivalent if $F’$ is obtained from $F$ by a sequence of applictions of EA-equivalence and inverses of permutations.

Functions $x^d$ and $x^{d’}$ over $\mathbb{F_{2^n}}$ are cyclotomic equivalent if

• $d’ = 2^i \cdot d \mod (2^n -1) $
• $d’ = 2^i / d mod (2^n-1)$ if $\gcd(d, 2^n-1)=1$

Relations Between Equivalences

Linear equivalences is particular case of affine equivalence Affine equivalence is a particular case of EQ-Equivalence EQ-equivalence is a perticulare case of EAI-equivalence. Cyclotomic equivalence is a particular case of EAI-equivalence

Invariants for Equivalences

APNNess, ABness, nonlinearity and differential uniformity are preserved by EAI-equivalence.

Algebraic degree is preserved by EA-equivalence but not by EAI-equivalence

Permutation property is preservedby cyclotomnic and affine equivalences (not by EA- or EAI- equivalences).

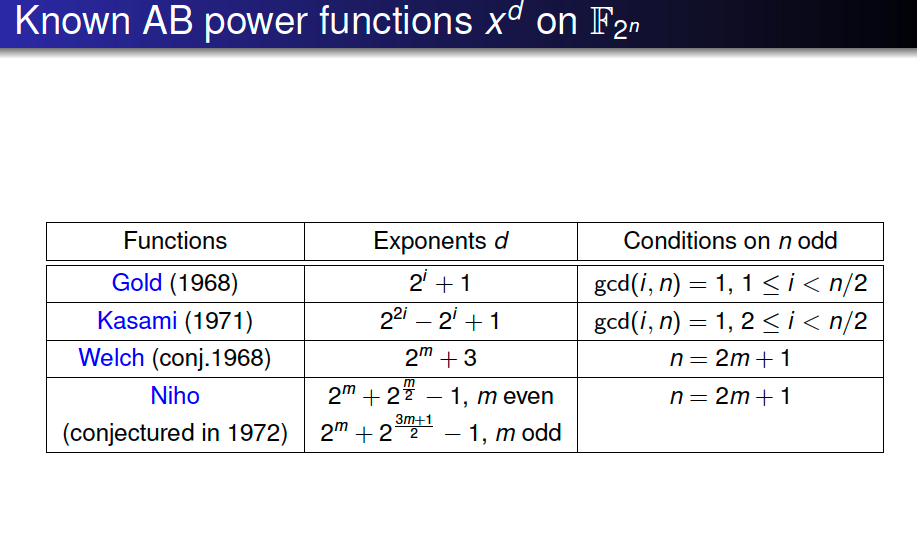
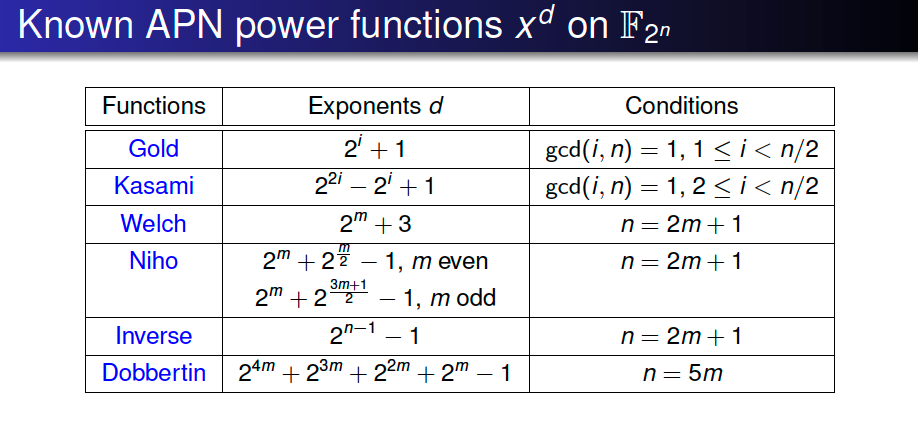
This list is up to cyclotomic equivalences and is conjectured complete (Dobbertin 1999)

For $n$ even the inveres function is differentally 4-uniform and maximally nonlinear and is used as S-box in AES with $n=8$.

CCZ-Equivalence

The graph of a function $F: \mathbb{F_{2^n}} \rightarrow \mathbb{F_{2^n}}$ is the set:

$$G_F = \{(x, F(x)) : x \in \mathbb{F_{2^n}}\}$$

$F$ and $F’$ are CCZ-equivalent if $\mathcal{L}(G_F) = G_{F’}$ for some permutation $\mathcal{L}$ of $\mathbb{F_{2^n} \times \mathbb{F_{2^n}}}$.

CCZ-equivalence

Preserves differential uniformity, nonlinearity, extended Walsh spectrum

EAI-equivalence is a particular case of CCZ-equivalence

Is more general than EAI-equivalence.

CCZ-equivalence for special functions

Two quadradic functions are CCZ-equivalenc if and only if they are EA-equivalent

Two power functions are CCZ-equivalent if and only if they are cylotomic equivalent

Two Boolean functions are CCZ-equivalent if and only if they are EA-equivalent.

Two bent funtions are CCZ-equivalent if and only if they are EA-equivalent.