Lecture: 21 - 22

[ Home ][ PDF ]

Topics: Boolean functions

Boolean and Vectorial Boolean Functions

Let $n$ and $m$ be positive integers. $\mathbb{F_2} = {0,1}$ be the field with 2 elements $\mathbb{F_2}^n$ be a $n$ dimentional vectorspace of $\mathbb{F_2}$ That is $\mathbb{F_2}^n$ is the set that contains all the vectors of 0’s and 1’s of length $n$.

Then we have boolean functions that are mappings

$$F: \mathbb{F_2}^n \rightarrow \mathbb{F_2}$$

Meaning from $\mathbb{F_2}^n$ info $\mathbb{F_2}$, mapping vectors of 0’s and 1’s of length $n$ info 0 or 1.

Vectorial boolean $(n,m)$-functions are mappings

$$F: \mathbb{F_2}^n \rightarrow \mathbb{F_2}^m$$

From $\mathbb{F_2}^n$ to $\mathbb{F_2}^m$

Application of Boolean Functions

The inital motivation for introduction of Boolean functions:

• fundamental mathematics
• mathematical logic

Modern application of Boolean functions:

• Reliability theory, multicriteria analysis, mathematical biology, image processing, theoretical physics, statistics.
• voting games, artificial intelligence, managment science, digital electronics, propositional logic,
• combinatorics
• coding theory, sequcen design, cryptography

On the number of Boolean functions

Let $BF_n$ be the set of all boolean functions: $F : \mathbb{F_2}^n \rightarrow \mathbb{F_2}$ for a given $n$. The number of possible Boolean functions for this $n$ is

$$|BF_n| = 2^{2^n}$$

which for $n = 8$ is compraable with the number of atoms in the universe.

n	4	5	6	7	8
$BF_n$	$2^{16}$	$2^{32}$	$2^{64}$	$2^{128}$	$2^{256}$
$\approx$	$6\cdot10^4$	$4\cdot10^9$	$10^{19}$	$10^{38}$	$10^{77}$

On the number of vectorial Boolean Functions

$BF_n^n$ is the set of vectorial Boolean Functions:

$$F: \mathbb{F_2}^n \rightarrow \mathbb{F_2}^n$$

The number of all these functions increasees even faster.

$$|BF_n^n| = 2^{n2^{n}}$$

n	4	5	6	7	8
$BF_n^n$	$2^{64}$	$2^{160}$	$2^{384}$	$2^{896}$	$2^{2048}$

Hence computer serach alone is not feasible for finding optimal Boolean functions for different applications.

Cryptographic properties of functions

S-Boxes are vectorial Boolean functions used in block ciphers to provide confusion. They should possess certain properties to ensure resitance of the ciphers to cryptographic attacks.

Main cryptographic attacks on block ciphers and corresponding properties of S-Boxes:

• Linear attack $\rightarrow$ Nonlinearity
• Differential attack $\rightarrow$ Differential uniformity
• Algebraic attack $\rightarrow$ Existence of low degree multivariate equations
• Higher order differential attack $\rightarrow$ Algebraic degree
• Interpolation attack $\rightarrow$ Univariate polynomial degree

Optimal Cryptographic Functions

Optimal Cryptographic functions are vectorial Boolean functions optimaly for primary cryptograhic criteria:

• UNIVERSAL
  • They define optimal objects in several branches of mathematics and information theory (coding theory, sequence design, projective geometry, combinatorics, commutative algebra)
• HARD-TO-GET
  • There are only a few known constructions
• HARD-TO-PREDICT
  • most conjectures are proven to be false

Binary expansion and representation of integers

Binary expansion of an integer k, $0 \leq k \leq 2^n$

$$k = \sum_{s=0}^{n-1} 2^sk_s$$

Where $k_s, 0 \leq k_s \leq 1$

2-Weight of k:

$$w_2(k) = \sum_{s=0}^{n-1} k_s$$

$v_k = (k_{n-1}, \dots , k_0)$ is the binary representation of $k$

Truth table representation of function

For $F: \mathbb{F_2}^n \rightarrow \mathbb{F_2}^m$ the sequence $(F(v_0), \dots , F(v_{2^n-1}))$ is called the truth table of $F$.

Example:

Truth table of $F: \mathbb{F_2}^3 \rightarrow \mathbb{F_2} : (0,1,0,0,0,1,0,1)$

$x_1$	$x_2$	$x_3$	$F(x_1, x_2, x_3)$
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

k	0	1	2	3	4	5	6	7
$F_{v_k}$	0	1	0	0	0	1	0	1

ANF representation of functions

ANF (Algebraic normal form) of $F : \mathbb{F_2}^n \rightarrow \mathbb{F_2}^m$ is a representation as a polynomial in $n$ variables with coefficient in $\mathbb{F_2}^m$

$$F(x_1, \dots, x_n) = \sum_{u\in \mathbb{F_2^n}} a_u \prod_{i=1}^{n} x_i^{u_i} , a_u \in \mathbb{F_2}^m, u = (u1, \dots, u_n)$$

The algebraic degree $d^o(F)$ of $F$ is the degree of its ANF. F is affine if $d^o(F) \leq 1$ * $F$ is quadratic if $d^o(F) \leq 2$

• affine : of, relating to, or being a transformation (such as a translation, a rotation, or a uniform stretching) that carries straight lines into straight lines and parallel lines into parallel lines but may alter distance between points and angles between lines

Example:

$$F(x_1, x_2, x_3) = x_1x_2x_2 + x_2x_3 + x_3$$ $$d^o(F) = 3$$

Boolean functions as Sums of Atomic functions I

If for $f_k : \mathbb{F_2}^n \rightarrow \mathbb{F_2}$ where $f(v_k) = 1$ and $f(v_j) = 0$ then for all $j \neq k$ then $f_k$ is atomic function. Decomposition of $f : \mathbb{F_2}^n \rightarrow \mathbb{F_2}$ as a sum of atomnic functions.

$$f = \sum_{k=0}^{2^n-1} \epsilon_k f_k, \epsilon_k \in \mathbb{F_2}$$

Example 1:

$F = (0, 1, 0, 0, 0, 1, 0, 1) = f_1 + f_5 + f_7$ on $\mathbb{F_2}^3$

k	$x_1$	$x_2$	$x_3$	$f(x)$
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	0
5	1	0	1	1
6	1	1	0	0
7	1	1	1	1

If $f: \mathbb{F_2}^n \rightarrow \mathbb{F_2}$ is an atomic function then: $f(x) = (x_1 + \epsilon_1) \dots (x_n + \epsilon_n), \epsilon_i \in \mathbb{F_2} $ and $d^o(f) = n$

Example:

$$f_1(x) = (1 + x_1)(1 + x_2)x_3$$ $$f_5(x) = x_1 (1 + x_2) x_3$$ $$f_7(x) = x_1x_2x_3$$ $$f(x) = f_1(x) + f_5(x) + f_7(x)$$ $$f(x) = x_1x_2x_3 + x_2x_3 + x_3$$

Remark: $ d^o(f) = n$ for $f: \mathbb{F_2}^n \rightarrow \mathbb{F_2}$ if and only if the number of nonzero $\epsilon_k$ in its decomposition of $ f = \sum_{k=0}^{2^n-1} \epsilon_k f_k, \epsilon_k \in \mathbb{F_2} $ is odd.

Univariate representation of functions

• univariate: characterized by or depending on only one random variable

Let $\mathbb{F_{2^n}}$ denote the finite field with $2^n$ elements. The univariate representation of $F: \mathbb{F_{2^n} \rightarrow \mathbb{F_{2^m}}}$ for $m|n$

$$F(x) = \sum_{i=0}^{2^n-1} c_ix^i, c_i \in \mathbb{F_{2^n}}$$

The univariate degree of $F$ is the degree of its univariate representation

Example: $F(x) = x^7 + \alpha x^6 + \alpha^2x^5 + \alpha^4x^3$

where $\alpha$ is a primitive element of $\mathbb{F_{2^3}}$ $F$ has univariate degree 7 and algebraic degree 3.

Algrebraic degree of univariate function

Algebraic degree in univariate representation of $F$.

$$F(x) = \sum_{i=0}^{2^n-1} c_ix^i, c_i \in \mathbb{F_{2^n}}$$ $$d^o(F) = \max\limits_{0\leq i < 2^n, c_j \neq 0} w_2(i)$$

Special functions

$F$ is linear if

$$F(x) = \sum_{i=0}^{n-1} b_ix^{2^i}$$

$F$ is affine if it is a linear funtion pluss a constatnt

$F$ is quadratic if for some affine $A$

$$F(x) = \sum_{i,j=0, i\neq j}^{n-1} b_{ij}x^{2^i+2^j} + A(x)$$

$F$ is power function or monomila if $F(x) = x^d$

$F$ is a permutation if it is a one-to-one map.

The inverse $F^{-1}$ of a permutation $F$ is s.t $F^{-1}(F(x)) = F(F^{-1}(x)) = x$

Trace and Component functions

Trace function from $\mathbb{F_{2^n}}$ to $\mathbb{F_{2^m}}$ for $n$ divisible by $m$

$$tr_n^m(x) = \sum_{i=0}^{n/m-1} x^{2^{im}}$$

Absolute trace funtion:

$$tr_n(x) = tr_n^1(x) = \sum_{i=0}^{n-1} x^{2^{i}}$$

For $F: \mathbb{F_{2^n}} \rightarrow \mathbb{F_{2^m}}$ and $v \in \mathbb{F_{2^m}^*}$

$$tr_m(vF(x))$$

is a component function of $F$

Hamming Weight and Hamming Distance

The hamming weight of $x = (x_1, \dots , x_2) \in \mathbb{F_2^n}$:

$$wt(x) = |\{i \in \{1, \dots, n\}| x_i \neq 0\}$$

For $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ its support:

$$\sup\limits_{f} = \{x \in \mathbb{F_2^n} | f(x) = 1\}$$

The Hamming weight of f: $wt(f) =

\sup_f

$

The Hamming distance between $f, g$: $\mathbb{F_2^n} \rightarrow \mathbb{F_2} : d(f,g) = wt(f +g)$

Proposition:

1. $d(f,g) =

   {x \in \mathbb{F_2^n} : f(x) \neq g(x)}

   $

2. $d(f,g+1) = 2^n - d(f,g)$
3. $d(f,g) + d(g,h) \geq d(f,h)$

Nonlinearity of Boolean Functions

From Wiki

In mathematics, more specifically in harmonic analysis, Walsh functions form a complete orthogonal set of functions that can be used to represent any discrete function—just like trigonometric functions can be used to represent any continuous function in Fourier analysis. They can thus be viewed as a discrete, digital counterpart of the continuous, analog system of trigonometric functions on the unit interval. But unlike the sine and cosine functions, which are continuous, Walsh functions are piecewise constant. They take the values −1 and +1 only, on sub-intervals defined by dyadic fractions. The system of Walsh functions is known as the Walsh system. It is an extension of the Rademacher system of orthogonal functions. Walsh functions, the Walsh system, the Walsh series, and the fast Walsh–Hadamard transform are all named after the American mathematician Joseph L. Walsh. They find various applications in physics and engineering when analyzing digital signals.

The nonlinerarity of $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$

$$N_f = \min\limits_{a\in\mathbb{F_2^n}, b \in \mathbb{F_2}} d(f, a\cdot x + b)$$

Where

$$a \cdot x$$ $$= (a_1, \dots, a_n) \cdot (x_1, \dots, x_n)$$ $$= a_1x_1 + a_2x_2+ \dots + a_nx_n$$

Walsh transform of $f$ is the function:

$$\lambda_f(u) = \sum_{x\in\mathbb{F_2^n}} (-1)^{f(x) + u\cdot x}, u \in \mathbb{F_2^n}$$

Walsh coefficients of $f$ are the values of $\lambda_f$ Walsh spectrum of $f$ is the multi-set of its Walsh Coefficients

Extended Walsh spectrum of $f$ is the mutli-set of absolute values of its Walsh coefficients.

Properties of Walsh Transform

• $\lambda_f(u) = \lambda_g(0)$ for $g(x) = f(x) + u \cdot x$

• $\lambda_f(u) = 2^n -2wt(f(x) + u \cdot x) = 2^n -2d(f(x), u \cdot x)$

• $wt(f) = 2^{n-1} - \frac{1}{2}\lambda_f(0)$

• $N_f = 2^{n-1} - \frac{1}{2}\max\limits_{u\in\mathbb{F_2^n}}

  \lambda_f(u)

  $

$$\sum_{u\in\mathbb{F_2^n}} \lambda_f(u)\lambda_f(u+v) = \begin{cases} 2^{2n} , \text{if } v = 0\\ 0, \text{ otherwise} \end{cases}$$

• Parseval’s equation

$$\sum_{u\in\mathbb{F_2^n}} (\lambda_f(u))^2 = 2^{2n}$$

• $\lambda(u) = 0 $ for $u \neq a$ and $(-1)^b 2^n$ otherwise if $f(x) = a\cdot x + b$

• $\lambda_{(f+1)}(u) = - \lambda_f(u)$

• $\lambda_g(u) = \lambda_f(u+a)$ if $g(x) = f(x) + a \cdot x$

• $\lambda_g(u) = (-1)^{a\cdot u} \lambda_f(u)$ if $g(x) = f(x + a)$

• $\lambda_h(u,v) = \lambda_f(u)\lambda_g(v)$ if $h(x,y) = f(x)+ g(y), f : \mathbb{F_2^n} \rightarrow \mathbb{F_2},g : \mathbb{F_2^m} \rightarrow \mathbb{F_2}$

Proof: (From slides)

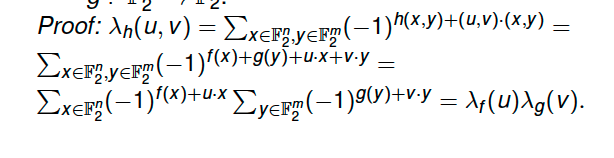
Inversion formula for Walsh Transform

Any function $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ is uniquely determined by its Walsh transform. That is, for any $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ we have:

$$(-1)^{f(u)} = 2^{-n} \sum_{x\in \mathbb{F_2^n}} \lambda_f(x)(-1)^{u\cdot x}$$

Bent functions

Bent functions exists if and only if $n$ is even

Covering radious bound fro the nonlinearity of a bolean function:

$$N_f \leq 2^{n-1} - 2^{n/2-1}$$

$N_f \leq 2^{n-1} - 2^{n/2-1}$ if and only if $\lambda(u) = \pm 2^{n/2}$ for any $u \in \mathbb{F_2^n}$

If $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ is bent den $d^o(f) =2$ for $n = 2$ and $d^o(f) \leq \frac{n}{2}$ for $n \geq 4$

Example of Bent funtions

$f(x) = x_1x_2$ on $\mathbb{F_2^2}, \lambda_f(u) = \pm2$

$f(x) = 1 + x_1x_2 + x_1x_3 + x_1x_4 + x_2x_3 + x_2x_4 + x_3x_4$ on $\mathbb{F_2^4},$ $\lambda_f(u) = 4$

Balanced funtions and derivatives

• $f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ is balanced if $wt(f) = 2^{n-1}$

• $f$ is balanced if and only if $\lambda_f(0) = 0$

• If $f$ is bent, then $f$ is not balanced. (PS: Bent only happens for even numbers of $n$)

• The derivative of $f$ in direction $a \in \mathbb{F_2^n}$ is

$$D_af(x) = f(x) + f(x+a)$$

$f: \mathbb{F_2^n} \rightarrow \mathbb{F_2}$ is called perfect nonlinear if $D_af$ is balanced for all $a\in \mathbb{F_2^n}$/{$0$}

$f$ is bent if and only if it is perfect nonlinear.

Bent functions and Extended affine-Equivalence

Boolean function $f,g$ on $\mathbb{F_2^n}$ are called extended affine equivalent if $g(x) = f(A(x) + a) + b \cdot x + c$ for $a,b \in \mathbb{F_2^n}, c \in \mathbb{F_2}$ and $A : \mathbb{F_2^n} \rightarrow \mathbb{F_2^n}$ is an affine permutation.

If no such transformation exists then $f,g$ are called EA-inequivalent

EA-Equivalent funtions have the same nonlinearity extende Walsh spectrum, algebraic degree

If $g$ is EA-equivealent to a bent function $f$, then $g$ is bent also.

Construction of Bent functions

Primary contructions include

Maiorana-McFarland constructions Dillon’s construction infinite classes in trace representation

Secondary constructions use known bent fuctinos asa building blocks.

Maiorana-McFarland constructions

Maiorana-McFarland constructions (MM-Class):

$$f: \mathbb{F_2^{n/2}} \times\mathbb{F_2^{n/2}} \rightarrow \mathbb{F_2}$$ $$f(x,y) = x \cdot \pi(y) + g(y)$$

Where $\pi$ is a permutation of $\mathbb{F_2^{n/2}}$ and $g$ is a Boolean function over $\mathbb{F_2^{n/2}}$.

Then $f$ is bent.

• Number of functions in MM-class is $2^{n/2}!2^{2^{n/2}}$
• There exist bent functions of any algebraic degree, $d, 2 \leq d \leq \frac{n}{2}$
• Every quadratic bent funtion is EQ-equivalent to MM function
• Every bent function with $n \leq 6$ is EQ-equivalent to MM function.

Dillon’s function

$f: \mathbb{F_2^{n/2}} \rightarrow \mathbb{F_2}$ is called $PS_{ap}$ or Dillon’s function if: $f(x,y) = g(\frac{x}{y})$ where $g: \mathbb{F_2^{n/2}} \rightarrow \mathbb{F_2}$ is balanced and $g(0) = 0$ $d^o(f) = n$

Trace Constructions

• Gold function: $f(x) = tr_n(ax^{2^i+1})$ is bent on $\mathbb{F_{2^n}}$ where $\frac{n}{\gcd(n,i)}$ is even and $a\in \mathbb{F_{2^n}}$ is not $2^i + 1$-th power.

• Kasami function: $f(x) = tr_n(ax^{2^{2i}-2^i+1})$ is bent on $\mathbb{F_{2^n}}$ where $\gcd(n,i) = 1$ is even and $a\in \mathbb{F_{2^n}}$ is not a cube.

• Dillons function: $f(x) = tr_n(ax^{j(2^{n/2-1})})$ is bent on $\mathbb{F_{2^n}}$ where $\gcd(j, 2^{n/2} +1)$ under some condition on $a$.

Example of a secondary construction of bent functions

Theorem:

Let $f: \mathbb{F_2^{n}} \rightarrow \mathbb{F_2}, g: \mathbb{F_2^m} \rightarrow \mathbb{F_2}, h: \mathbb{F_2^{n+m}} \rightarrow \mathbb{F_2}$ s.t $h(x,y) = f(x) + g(y)$ and $n,m$ are even. Then $h$ is bent if and only if $f$ and $g$ are bent.

Proof: Since $\lambda_h(u,v) = \lambda_f(y)\lambda_g(v)$

Example: $f: \mathbb{F_2^2} \rightarrow \mathbb{F_2}, f(x_1, x_2) = x_1, x_2$ is Bent (Se bent example).

Then $h: \mathbb{F_2^{2n}} \rightarrow \mathbb{F_2}$

$$h(x_1, \dots, x_n) = x_1x_2 + x_3x_4 + \dots +x_{2n-1}x_{2n}$$

is bent.