Lecture: 13 - 14

[ Home ][ PDF ]

Topics: Characterization of Finite Fields and Roots of Irreducible polynomials

Important lecture as it contains various fundamental properties of finite fields and a description of methonds for constructing finite fields.

The field of integers modulo a prime number is, the most familiar example of a finite field.

Characterization of finite fileds show that every finite filed is of prime-power order and that for every prime power there exists a finite filed whose number of elemest is exactly that primer power (conversly).

Finite fiels with the same number of elemensts are isomorphic and may therefore be identified.

Irreducible polynomials leads to an interpretation of finite fields as spliltting fields of irreducible polynimilas and on traces, norms and bases relative to field extensions.

Characterization of Finite Fields

For every prime $p$ the residue class ring $\mathbb{Z}/(p)$ forms a finite field with $p$ elements. (Theorem 1.38).

This may be identitfied with the Galiis field $\mathbb{F_p}$ of order $p$. Definition (1.41).

The fields $\mathbb{F_p}$ play an important role in general field theory since every field of characteristic $p$ must contain an isomorphic copy of $\mathbb{F_p}$ (Theorem 1.78), and can be thought of as an extension of $\mathbb{F_p}$.

This observation together with the fact that every finite fields has prime characteristic (Corollary 1.45), is fundamental for the calssification of finite fields.

Lemma 2.1

Lemma with description of the nu,ner of elements in a finite field by the number of elements of its subfield and edfree over this subfield.

Let $F$ be a finite fileds containg a subfield $K$ with $q$ elements. Then $F$ has $q^m$ elements, where $m = [F:K]$

Proof

$F$ is a vector space over $K$, and since $F$ is finite, it is finite-dimentional as a vector space over $K$. If $[F:K] =m$, then $F$ has a basis over $K$ consisting of $m$ elements, say $ b_1,b_2,\dots , b_m$. Thus every element of $F$ ca be uniquely represented in the form $ a_1b_1 + a_2b_2 + \dots + a_mb_m $ wherre $ a_1,a_2,\dots ,a_m \in K$. Since each $a_i$ can have $q$ values, $F$ has exactly $q^m$ elements.

Lemma 2.2

Lemma with description of the number of elements in a finite fields as $p^n$ with $p$ as a prime and $n$ a positive integer.

Let $F$ be a finite field, Then $F$ has $p^n$ elements, where the prime $p$ is the characteristic of $F$ and $n$ is the degree of $F$ over its prime subfield.

Proof

Since $F$ is finite, its characteristic is a prime $p$ according to Corollary 1.45. Therefore the prime subfield $K$ of $F$ is isomorphic to $\mathbb{F_p}$ by Theorem 1.78 and thus contains $p$ elements. The rest from lemma 2.1.

Starting from the prime fields $\mathbb{F_p}$ we can construct other finite fields by the process of root adjunction.

If $f \in \mathbb{F_p}[x]$ is an irreducible polynimial over $\mathbb{F_p}$ with degree $n$, then by adjoining a root of $f$ to $\mathbb{F_p}$ we get a finite fields with $p^n$ elements.

However at this stage it is not clear whether for every positive integer $n$ there exists a irreducible polynomial in $\mathbb{F_p}[x]$ of degree $n$. In order to etablish that for every prime $p$ and every $n \in \mathbb{N}$ there is a finite filed with $p^n$ elements, we use an approach stuggested by the following results.

Lemma 2.3

If $F$ is a finite field with $q$ elements, then every $a\in F$ satifies $a^q = a$.

Proof

The identity $a^q = a$ is trivial for $a=0$. On the other hand the nonzero erlement of $F$ form a group of order $q-1$ under multiplication. Thus $a^{q-1} = 1$ for all $a \in F$ with $a \neq 0$ and multiplication by $a$ yields the desired result.

Lemma 2.4

If $F$ is a finite field with $q$ elements and $K$ is a subfield of $F$, then the polynomial $x^q - x$ in $K[x]$ factors in $F[x]$ as:

$$x^q-x = \prod_{a \in F} ( x - a)$$

and $F$ is a splitting field of $x^q-x$ over $K$.

Proof

The polynomial $x^q -x$ of degree $q$ has at most $q$ roots in $F$. By lemma 2.3 we know that such roots, all the elements of $F$. Thus the givenn polynomilal splits in $F$ in the indicated manner, and it cannot split in any smaller field.

We are now able to prove the main characterization theorem for finite fields, the leading idea being contained in Lemma 2.4.

Theorem 2.5 Existence and Uniqueness of Finite Fields

For every prime $p$ and every positive integer $n$ there exists a finite field with $p^n$ elements. Any finite field with $q = p^n$ elements is isomorphic to the splitting field of $x^q -x$ over $\mathbb{F_q}$

Proof

For $q = p^n$ consider $x^q -x$ in $\mathbb{F_p}[x]$ and let $F$ be its splitting field over $\mathbb{F_p}$. This polynomial has $q$ distinct roots in $F$ since its derivative is $qx^{q-1} -1 = -1 $ in $\mathbb{F_q}[x]$ and so can have no common root with $x^q-x$

Let $S = { a\in F: a^q -a = 0 } $. Then $S$ is a subfield of $F$ since: i) $S$ contains 0 and 1; ii) $a,b \in S$ implies by Theorem 1.46 that $(a - b)^q = a^q -b^q = a-b$ and so $a-b \in S$ iii) for $a,b \in S$ and $b \neq 0$ we have $(ab^{-1})^q = a^q b^{-q} = ab^{-1}$ and so $ab^{-1} \in S$.

But on the other hand $x^q-x$ must split in $S$ since $S$ contains all its roots. This $F=S$ and since $S$ has $q$ elemenst, $F$ is a finite field with $q$ elements.

Uniqueness : Let $F$ be a finite field of $x^q-x$ over $\mathbb{F_p}$. Thus the desired result is consequence of the uniqueness (up to isomorhphism) of splitting fields which was noted in Theorem 1.91

The uniqueness part of Theorem 2.5 provieds the justification for speaking of the finite field (or theGalois field) with $q$ elements, or the finite filed of order $q$

We shalle denote this field buy $\mathbb{F_q}$ where it is of course understood that $q$ is a power of the prime characterisitc $p$ of $\mathbb{F_q}$.

Theorem 2.6 (Subfield Criterion)

Let $\mathbb{F_q}$ be the finite field with $ q = p^n$ elements. Then every subfield of $\mathbb{F_q}$ has order $p^m$ where $m$ is a positive divisor of $n$. Conversely, if $m$ is a positive divisor of $n$, then there is exactly one subfield of $\mathbb{F_q}$ with $p^m$ elements.

Proof

It is clear that a subfield $K$ of $\mathbb{F_q}$ has order $p^m$ for some positive integer $m \leq n$. Lemma 2.1 shows that $q = p^n$ must be a power of $p^m$, and so $m$ is necessarily a divisor of $n$.

Conversely, if $m$ is a positive divisor of $n$, then $p^m - 1$ divides $p^n -1$ and so $x^{p^{m}-1} -1 $ divides $x^{p^{n}-1} -1 $ in $\mathbb{F_p}[x]$. Consequently, $x^{x^m}-x$ divides $x^{p^n}-x = x^q-x$ in $\mathbb{F_q}$. Thus ever root of $x^{p^n} -x$ is a root of $x^q-x$ and so belongs to $\mathbb{F_q}$. If follows that $\mathbb{F_q}$ must contain as a subfield a splitting field of $x^{p^m}-x$ over $\mathbb{F_q}$ and as we have seen in the proof of Theorem 2.5, such a splitting field has order $p^m$. If there werer two dstinct subfields of order $p^m$ in $\mathbb{F_q}$, they would together contain more than $p^m$ roots of $x^{p^m}-x$ in $\mathbb{F_q}$, an obvious contraditcion.

The proof of Theorem 2.6, shows that the unique subfield of $\mathbb{F_{q^n}}$ of order $p^m$, where $m$ is a positive divisior of $n$, consists precisely of the roots of the polynomial $x^{p^m} -x \in \mathbb{F_p}[x]$ in $\mathbb{F_{p^n}}$

2.7 Example of a field

The subfield of the finite field $\mathbb{F_{2^30}}$ can be determined by listting all positive divisors of 30. The containment relastions between these various subfields are displayed in the following diagram.

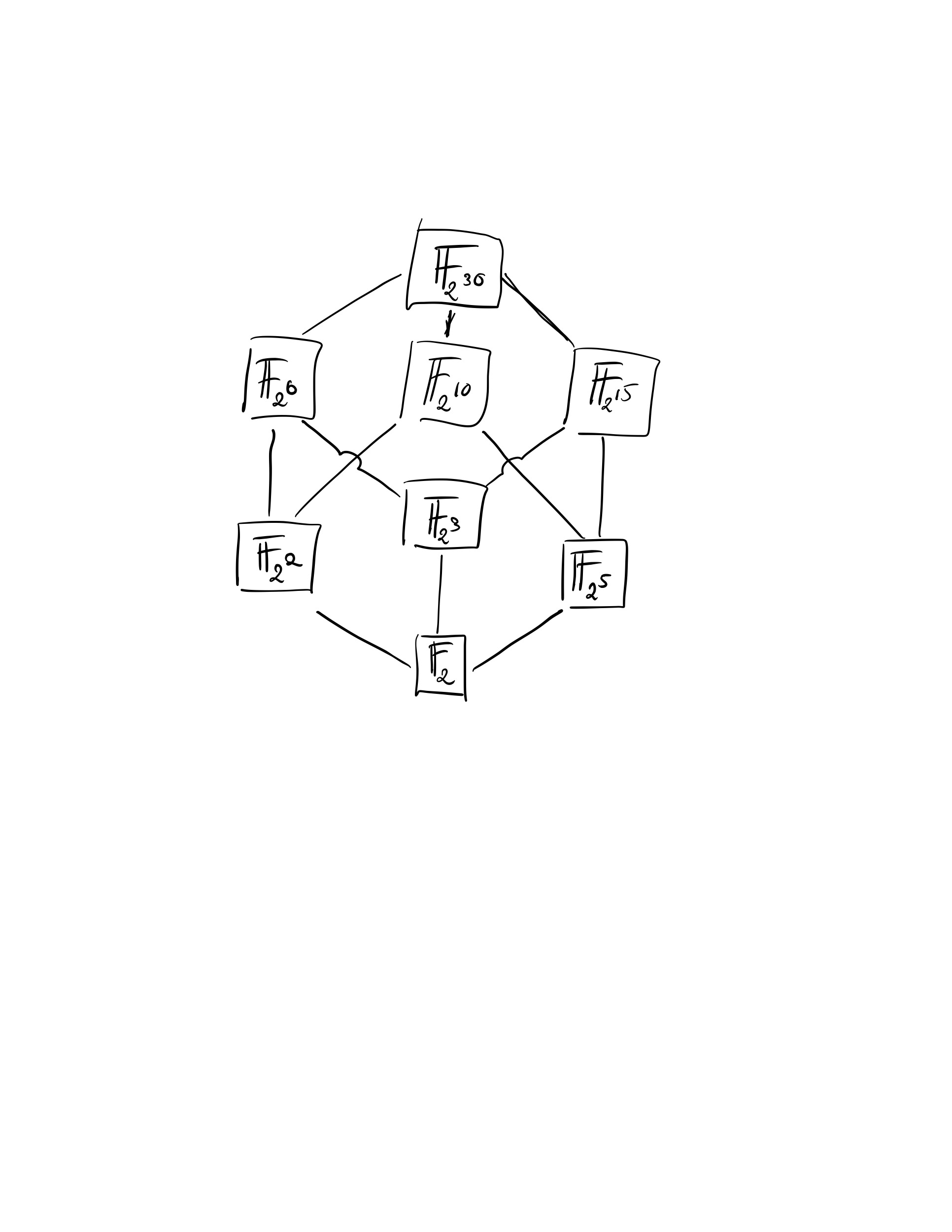
By Theorem 2.6, the containment relations are equivalent to divisibility relastions among the positive divisors of 30.

For a finite filed $\mathbb{F_q}$ we denote by $\mathbb{F_q}^*$ the multiplicative gorup of nonzero elements of $\mathbb{F_q}$. The following result enunciates a useful property of this group.

Theorem 2.8

For every finite field $\mathbb{F_q}$ the multiplicative group $\mathbb{F_q}^*$ of nonzero elements of $\mathbb{F_q}$ is cyclic.

Proof

We may assume $q \geq 3 $. Let $h = p_{1}^{r_1} p_{2}^{r_2} \dots p_{m}^{r_m}$ be the prime factor decomposition of the order $h = q -1$ of the group $\mathbb{F_q}^*$ For every $i, 1 \leq i \leq m$ , the polynomila $x^{h/p_i}-1$ has at most $h/p_i$ roots in $\mathbb{F_q}$

Since $h/p_i < h $ it follows that there are nonzero elements in $\mathbb{F_q}$ that are not roots of this polynomial. Let $ a_i$ be such an element and set $b_i = a_i^{h/p_i^{r_i}}$. We have $b_i^{p_i^{r_i}} = 1 $ hence the order of $b_i$ is a divisor of $p_i^{r_i}$ and is therefor of the form $p_i^{s_i}$ with $0 \leq s_i \leq r_i$. On the other hansd

$$b_i^{p_i^{r_i-1}} = a_i^{h/p_i} \neq 1$$

and so the order of $b_i$ is $p_i^{r_i}$.

We clain that the element $b = b_1b_2\dots b_m$ has order $h$. Suppose on the contrary, that the order of $b$ is a proper devisor of $h$ and is therefor a divisor of at least one of the $m$ integers $h/p_i, 1 \leq i \leq m$, say of $h/p_i$, then we have:

$$1 = b^{h/p_i} = b_1^{h/p_1} b_2^{h/p_1} \dots b_m^{h/p_1}$$

Now if $2 \leq i \leq m $ then $p_i^{r_i}$ divides $h/p_1$ and hence $b_i^{h/p_1} = 1$. Therefor $b_1^{h/p_1} = 1$. This implieds that the order of $b_1$ must divide $h/p_1$, which is impossible since the order og $b_1$ is $p_1^{r_1}$ Thus $\mathbb{F_q}^*$ is a cyclic group with generator $b$.

2.9 Definitions Primitive element

A generator of the cyclic group $\mathbb{F_q}^*$ is called a primitive element of $\mathbb{F_q}$

It follows from Theorem 1.15(v) that $\mathbb{F_q}$ containts $\phi(q-1)$ primitive elements, where $\phi$ is Euler’s function. The existence of primitive elements can be used to show a result that implies, in particular, that every finite field can be thought of as a simple algebraic extension of its prime subfield.

2.10 Theorem

Let $\mathbb{F_q}$ be a finite filed and $\mathbb{F_r}$ a finite extension field. Then $\mathbb{F_r}$ is a simple algebraic extension of $\mathbb{F_q}$ and every primitive element of $\mathbb{F_r}$ can serve as a defining element of $\mathbb{F_r}$ over $\mathbb{F_q}$.

Proof

Let $\delta$ be a primitive element of $\mathbb{F_r}$. We clearly have $\mathbb{F_q}(\delta) \subseteq \mathbb{F_Rr}$. On the other hand, $\mathbb{F_q}(\delta)$ contains $0$ and all powers of $\delta$, and so all elements of $\mathbb{F_r}$. Therefor $\mathbb{F_r} = \mathbb{F_q}(\delta)$

2.11 Corollary

For every finite field $\mathbb{F_q}$ and every positive integer $n$ there exists an irreducible polynomial in $\mathbb{F_q}[x]$ of degree $n$.

Proof

Let $\mathbb{F_r}$ be an extension field of $\mathbb{F_q}$ of order $q^n$, so that $[\mathbb{F_r}: \mathbb{F_q}] = n$. By Theorem 2.10 we have $\mathbb{F_r} = \mathbb{F_q}(\delta)$ for some $\delta \in \mathbb{F_r}$ Then the minimal polynomial of $\delta$ over $\mathbb{F_q}$ is an irreducible polynomial in $\mathbb{F_q}[x]$ of degree $n$, according to Theorems 1.82(i) and 1.86(ii).

Roots of Irreducible polynomials

In this section we collect some information about the set of roots of an irreducible polynomial over a finite field

2.12 Lemma

Let $f \in \mathbb{F_q}[x]$ be an irreducible polynomials over a finite field $\mathbb{F_q}$ and let $\alpha$ be a root of $f$ in an extension field of $\mathbb{F_q}$. Then for a polynomial $h \in \mathbb{F_q}[x]$ we have $h(\alpha) = 0$ if an only if $f$ divides $h$.

Proof

Let $a$ be the leading coefficient of $f$ and set $g(x) = a^{-1}f(x)$ Then $g$ is a monic irreducible polynomial in $\mathbb{F_q}[x]$ with $g(\alpha)=0$ and so it is the minimal polynomial of $\alpha$ over $\mathbb{F_q}$ in the sens of Definition 1.81. The rest follows from Theorem 1.82(ii).

2.13 Lemma

Let $f\in \mathbb{F_q}[x]$ be an irreducible polynomial over $\mathbb{F_q}$ of degree $m$. Then $f(x)$ divdes $x^{q^n}-x$ if and only if $m$ divides $n$.

Proof

Suppose $f(x)$ divides $x^{q^n}-x$. Let $\alpha$ be a root of $f$ in the splitting field of $f$ over $\mathbb{F_q}$ Then $\alpha^{q^n} = \alpha$, so that $\alpha \in \mathbb{F_{q^n}}$. It follows that $\mathbb{F_q}(\alpha)$ is a subfield of $\mathbb{F_{q^n}}$.

But since $[\mathbb{F_q}(\alpha) : \mathbb{F_q}] = m$ and $[\mathbb{F_{q^n}} : \mathbb{F_q}] = n$, Theorem 1.84 shows that $m$ divides $n$. Conversely, if $m$ divides $n$, then Theorem 2.6 implies that $\mathbb{F_{q^n}}$ contains $\mathbb{F_{q^n}}$ as a subfield. If $\alpha$ is a root of $f$ in the splitting field of $f$ over $\mathbb{F_q}$, then $[\mathbb{F_q}(\alpha) : \mathbb{F_q}] = m$ and so $\mathbb{F_q}(\alpha) = \mathbb{F_{q^m}}$.

Consequently, we have $\alpha \in \mathbb{F_{q^n}}$, hence $\alpha^{q^n} = \alpha$, and thus $\alpha$ is a root of $x^{q^n}-x \in \mathbb{F_q}[x]$ We infer then from Lemma 2.12 that $f(x)$ divides $x^{q^n}-x$

2.14 Theorem

If $f$ is an irreducible polynomial in $\mathbb{F_q}[x]$ of degree $m$, then $f$ has a root $\alpha$ in $\mathbb{F_q^m}$. Furthermore all the roots of $f$ are simple and are given by the $m$ distinc elements $\alpha, \alpha^q, \alpha^{q^2}, \dots, \alpha^{q^{m-1}}$ of $\mathbb{F_{q^m}}$.

Proof

Let $\alpha$ be a root of $f$ in the splitting field of $f$ over $\mathbb{F_q}$. Then $[\mathbb{F_q}(\alpha) : \mathbb{F_q} ] = m$ , hence $\mathbb{F_q}(\alpha) = \mathbb{F_{q^m}}$ and in particular $\alpha \in \mathbb{F_{q^m}}$. Next we show that if $\beta \in \mathbb{F_{q^m}}$ is a root of $f$, then $\beta^q$ is also a root of $f$. Write $f(x) = a_mx^m + \dots + \a_1x+a_0$ with $a_i \in \mathbb{F_q}$ for $0 \leq i \leq m$. Then, using Lemma 2.3 and Theorem 1.46, we get:

$$f(\beta^q) = a_m\beta^{qm} + \dots + a_q\beta^q+ a_0$$ $$= a_m^q\beta^{qm} + \dots + a_1^q\beta^q + a_0^q$$ $$= (a_m\beta^m + \dots + a_1\beta + a_0 )^q$$ $$= f(\beta)^q$$ $$= 0$$

Therefor, the elements $\alpha, \alpha^a, \alpha^{q^2}, \dots, \alpha^{q^{m-1}}$ are roots of $f$. It remains to prove that these elements are distinct. Suppose, on the contrary, that $\alpha^{q^j} = \alpha^{q^k}$ for some integers $j$ and $k$ with $0 \leq j < k \leq m -1$ By raising this identity to the power of $q^{m-k}$ we get:

$$\alpha^{q^{m-k+j}} = \alpha^{q^m} = \alpha$$

It follows then from Lemma 2.12 that $f(x)$ divides $x^{q^{m-k+j}}- x$. By Lemma 2.13, this is only possible if $m$ divides $m-k+j$. But we have $0 < m-k+j < m$, and so we arrive at a contradiction.

2.15 Corollary

Let $f$ be an irreducible polynomial in $\mathbb{F_q}[x]$ of degree $m$. Then the splitting field of $f$ over $\mathbb{F_q}$ is given by $\mathbb{F_{q^m}}$.

Proof: Theorem 2.14 shows that $f$ splits in $\mathbb{F_{q^m}}$. Furthermore $\mathbb{F_q}(\alpha, \alpha^q, \alpha^{q^2}, \dots, \alpha^{q^{m-1}}) = \mathbb{F_q}(\alpha) = \mathbb{F_{q^m}}$ for a root $\mathbb{\alpha}$ of $f$ in $\mathbb{F_{q^m}}$ where the seciond identity is taken from the proof of Theorem 2.14.

2.16 Corollary

Any two irreducible polynomials in $\mathbb{F_q}[x]$ of the same degree have isomorphic splitting fields.